[Computer] 2진법, 8진법, 10진법, 16진법 변환
정보 표현 단위
비트(Bit) - 바이트(Byte) - 워드(Word)
- 컴퓨터는 2진수로 데이터를 표현하는 단위, 가장 작은 단위의 데이터 크기인 비트(Bit)를 사용합니다
- 1바이트(Byte)는 8비트, 1바이트가 표현가능한 패턴은 2^8, 256가지 (0~255)
- 컴퓨터의 종류에 따라 2,4, n 바이트로 구성됨, 보통은 4바이트(32Bit)가 많이 쓰입니다

10진수 <-> 2진수, 8진수, 16진수
2진수 <-> 10진수
2진수의 가장 오른쪽부터 2^0, 왼쪽으로 갈수록 2^n씩 높아집니다
(11001) (2진수) -> 1 × 2^4 + 1 × 2^3 + 0 × 2^2 + 0 × 2^1 + 1 × 2^0
= 16 + 8 + 0 + 0 + 1 = (25) (10진수)
10진수를 2로 나누어, 나누어 떨어진 나머지를 역순으로 읽으면 2진수
(41) (10진수)
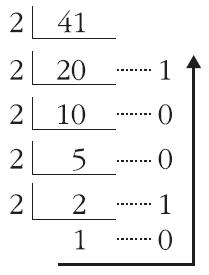
1 × 2^5 + 0 × 2^4 + 1 × 2^3 + 0 × 2^2 + 0 × 2^1 + 1 × 2^0 = (101001) (2진수)
8진수 <-> 10진수
8진수의 가장 오른쪽부터 8^0, 왼쪽으로 갈수록 8^n씩 높아집니다
(613) (8진수) -> 6 × 8^2 + 1 × 8^1 + 3 × 8^0
= 384 +8 + 3 = (395) (10진수)
10진수를 8로 나누어, 나누어 떨어진 나머지를 역순으로 읽으면 8진수
(314) (10진수)
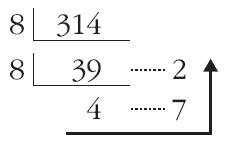
= 4 × 8^2 + 7 × 8^1 + 2 × 8^0 = (472) (8진수)
16진수 -> 10진수
16진수의 가장 오른쪽부터 16^0, 왼쪽으로 갈수록 16^n씩 높아집니다
(12e0) (16진수) -> 1 × 16^3 + 2 × 16^2 + e(14) × 16^1 + 0 × 16^0
= 4096 + 512 + 224 + 0 = (4832) (10진수)
10진수를 16으로 나누어, 나누어 떨어진 나머지를 역순으로 읽으면 16진수
(958) (10진수)

= 3 × 16^2 + b(11) × 16^1 + e(14) × 16^0 = (3be) (16진수)
2진수 <-> 8진수, 16진수
2진수 <-> 8진수
2진수의 가장 오른쪽부터 3비트씩 묶은 후, 분할된 2진수를 10진수로 변환합니다
(110010111110) (2진수) -> (110 010 111 110) -> (6 2 7 6) -> (6276) (8진수)
(10011001) (2진수) -> (-10 011 001) -> (2 3 1) -> (231) (8진수)
8진수를 2진수로 변환하려면 위 방법과 반대로 8진수의 각 자리를 3비트의 2진수로 변환합니다
(1374) (8진수) -> (1 3 7 4) -> (001 011 111 100) -> (001011111100) (2진수)
(606) (8진수) -> (6 0 6) -> (110 000 110) -> (110000110) (2진수)
2진수 -> 16진수
2진수의 가장 오른쪽부터 4비트씩 묶은 후, 분할된 2진수를 10진수로 변환합니다
(0011001011111000) (2진수) -> (0011 0010 1111 1000) -> (3 2 15(f) 8) -> (32f8) (16진수)
(1101001010) (2진수) -> (--11 0100 1010) -> (3 4 10(a) -> (34a) (16진수)
16진수를 2진수로 변환하려면 위 방법과 반대로 16진수의 각 자리를 4비트의 2진수로 변환합니다
(a626) (16진수) -> (a 6 2 6) -> (1010 0110 0010 0110) -> (1010011000100110) (2진수)
(ca) (16진수) -> (c a) -> (1100 1010) -> (11001010) (2진수)
8진수 <-> 16진수
8진수와 16진수간의 변환은 먼저 2진수로 변환한 후 위 글을 참고하여 계산하면 됩니다
진수변환해주는 사이트!
직접 계산해보고 맞는지 확인해 봅시다
Base calculator | math calculators
www.rapidtables.com